-
题目大意
- 我们已经学会了 N 种不同的游泳技术。对于每种技术 \(i\) ，每秒前进 \(A_{i}\) 米，并消耗 \(B_{i}\) 单位的体力。注意，我们可以任意调整每种技术的使用时长 \(t_i\) ，其中 \(t_i\) 是一个实数
- 现在，我们面临 \(Q\) 次询问，每次询问指定距离终点的距离 \(C_j\) 和体力限制 \(D_j\) 。我们需要确定是否在体力限制下到达终点。如果可以，求出所需的最短时间。
- （符号使用与原题略有差异）
- 数据规模：
- \(1 <= N, Q <= 2 \times 10^5\)
- \(1 <= A_i, B_i, C_j, D_j <= 10^9\)
-
题目分析
- 鉴于数据规模庞大，并且时间 \(t_i\) 是实数，传统的动态规划方法不适用。在处理每次询问时，我们需要同时考虑距离、体力和时间三个变量。一个有效的方法是转化这些变量为单位时间内的距离（即速度）和单位时间内的体力消耗。如果单位时间内的距离大于单位时间内的体力消耗，那么理论上我们可以到达终点。接下来的目标是在所有可能的情况中找到最大的速度，作为最终答案。
以两种游泳技术（N=2）为例进行具体分析。假设在总游泳时间中，技术1和技术2的使用时间比例分别为 \(p\) 和 \(1-p\) （其中 \(0 \leq p \leq 1\) ）。在这种情况下，每秒前进距离为 \(A_1 \cdot p + A_2 \cdot (1 - p)\) ，体力消耗为 \(B_1 \cdot p + B_2 \cdot (1 - p)\) 。
从几何角度看，组合这两种游泳技术的速度与体力消耗 \((A_x, B_x)\) 为 \((A_1, B_1) \cdot p\) 和 \((A_2, B_2) \cdot (1 - p)\) 的向量和，其可能的取值位于以 \((A_1, B_1)\) 和 \((A_2, B_2)\) 为端点的线段上的任意一点。
对于具体询问 \((C_i, D_i)\) ，为了确保“在到达终点之前不能耗尽体力”，我们需要找到的点必须位于斜率为 \(D_i/C_i\) 的射线与x轴之间的夹角内。通过这种方式，我们可以确定是否有可能在给定的体力限制下完成指定的距离，并找到速度最快的点。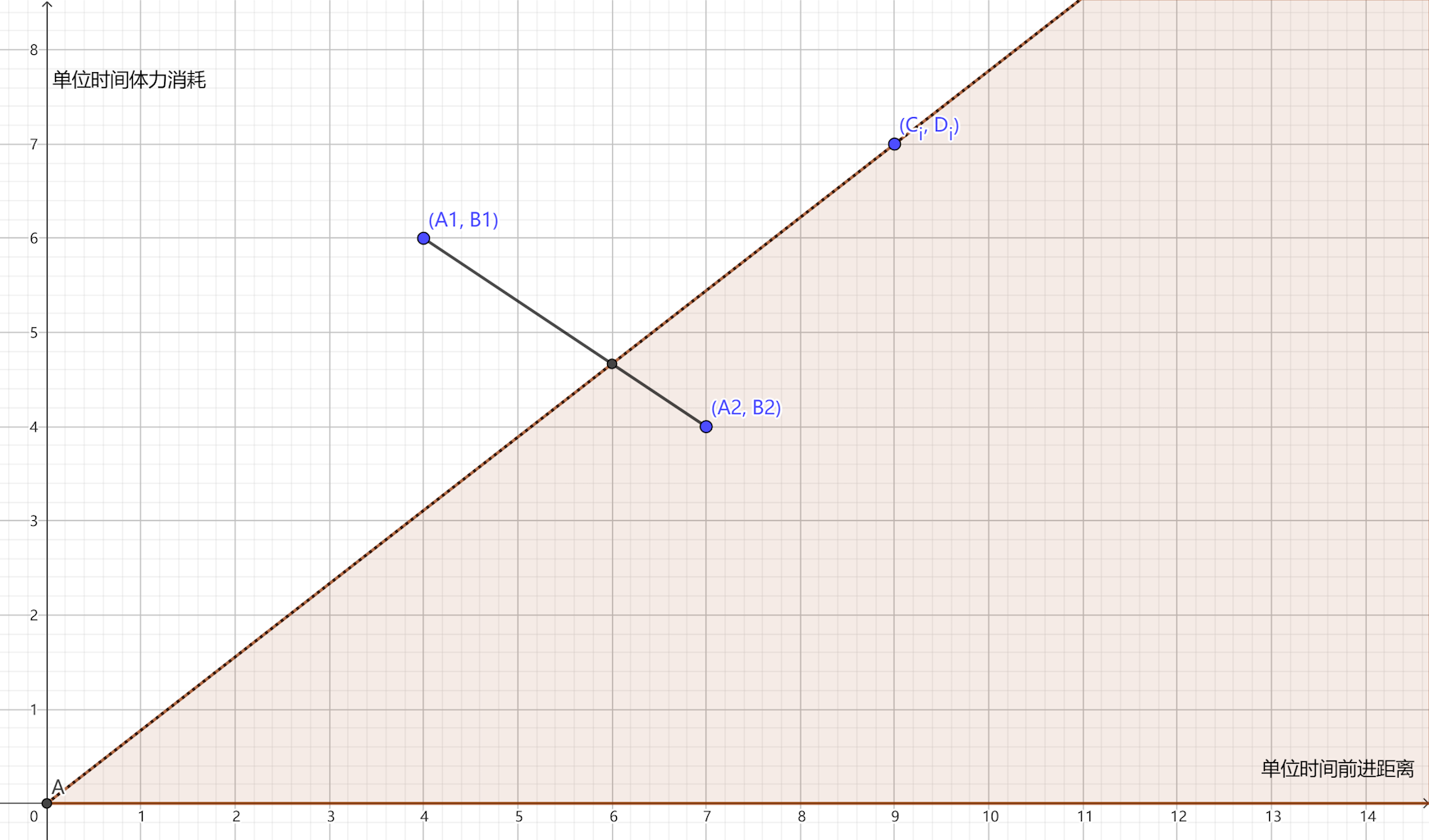 
- 对于多种游泳技术的组合，情况会更复杂一些。我们将所有游泳技术视为一组向量 \((A_1, B_1), (A_2, B_2), \ldots, (A_n, B_n)\) 和一组对应的权重 \(p_1, p_2, \ldots, p_n\) ，其中 \(\sum_{i=1}^n p_i = 1\) 并且每个 \(p_i \geq 0\) ，那么这些向量的加权和 \(\sum_{i=1}^n p_i (A_i, B_i)\) 定义了一个在二维空间中的凸多边形，称为这些向量的凸包。
- 我们可以用稍微详细一点的数学来解释这一过程：
-
向量的线性组合
- 首先，定义向量 \(\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n\) 在二维空间中的位置。每个向量 \(\mathbf{v}_i\) 可以表示为从原点到点 \((x_i, y_i)\) 的箭头。
当我们考虑这些向量的线性组合时： \(\sum_{i=1}^n \lambda_i \mathbf{v}_i\)
其中，每个 \(\lambda_i\) 是一个实数系数，我们实际上在描述一个新向量，这个向量是通过在每个原向量上“拉伸”或“压缩”（取决于 \(\lambda_i\) 的正负和大小），然后将结果相加得到的。这种线性组合在几何上定义了一个点的集合。
- 首先，定义向量 \(\mathbf{v}_1, \mathbf{v}_2, \ldots, \mathbf{v}_n\) 在二维空间中的位置。每个向量 \(\mathbf{v}_i\) 可以表示为从原点到点 \((x_i, y_i)\) 的箭头。
当我们考虑这些向量的线性组合时： \(\sum_{i=1}^n \lambda_i \mathbf{v}_i\)
-
凸组合与凸多边形
- 当这些系数 \(\lambda_i\) 都非负且和为1（即 \(\lambda_i \geq 0\) 且 \(\sum_{i=1}^n \lambda_i = 1\) ），我们称这样的线性组合为凸组合。凸组合具有重要的几何特性：它定义的点一定位于这些向量端点所形成的凸多边形内部或边界上。
-
凸多边形的形成
-
- 边界的构成：如果你只考虑两个向量 \(\mathbf{v}_1\) 和 \(\mathbf{v}_2\) ，那么它们的凸组合会形成一条连接两点 \((x_1, y_1)\) 和 \((x_2, y_2)\) 的线段。这条线段是直线，因为所有的组合点都直接通过两点间的直线路径互相连结。
-
- 扩展到多个向量：当你有三个或更多向量时，通过考虑任意两个向量的所有凸组合（即所有可能的线段），然后再将这些线段的结果进行组合，最终你将覆盖一个多边形区域。这个区域是由最外围的向量点定义的，这些点在几何上构成了凸多边形的顶点。
-
- 数学描述：在数学上，这个区域可以看作是所有可能的 \(\lambda_i\) 值（符合凸组合条件）下的 \(\sum_{i=1}^n \lambda_i \mathbf{v}_i\) 的集合。由于每个 \(\lambda_i\) 都保证非负且和为1，凸多边形的任意内部或边界点都可以通过这样的组合表示，且不会有任何点“凸出”于这个定义的多边形之外，这正是凸性质的体现。
-
-
- 类似于仅涉及两个点的简单情况，为了解决问题，我们需要找到凸多边形内与 \(x\) 轴之间斜率为 \(D_i/C_i\) 的射线包围的区域（即凸包中的深色部分）。我们进一步需要找出该部分中在 \(x\) 轴上取得最大值的点。
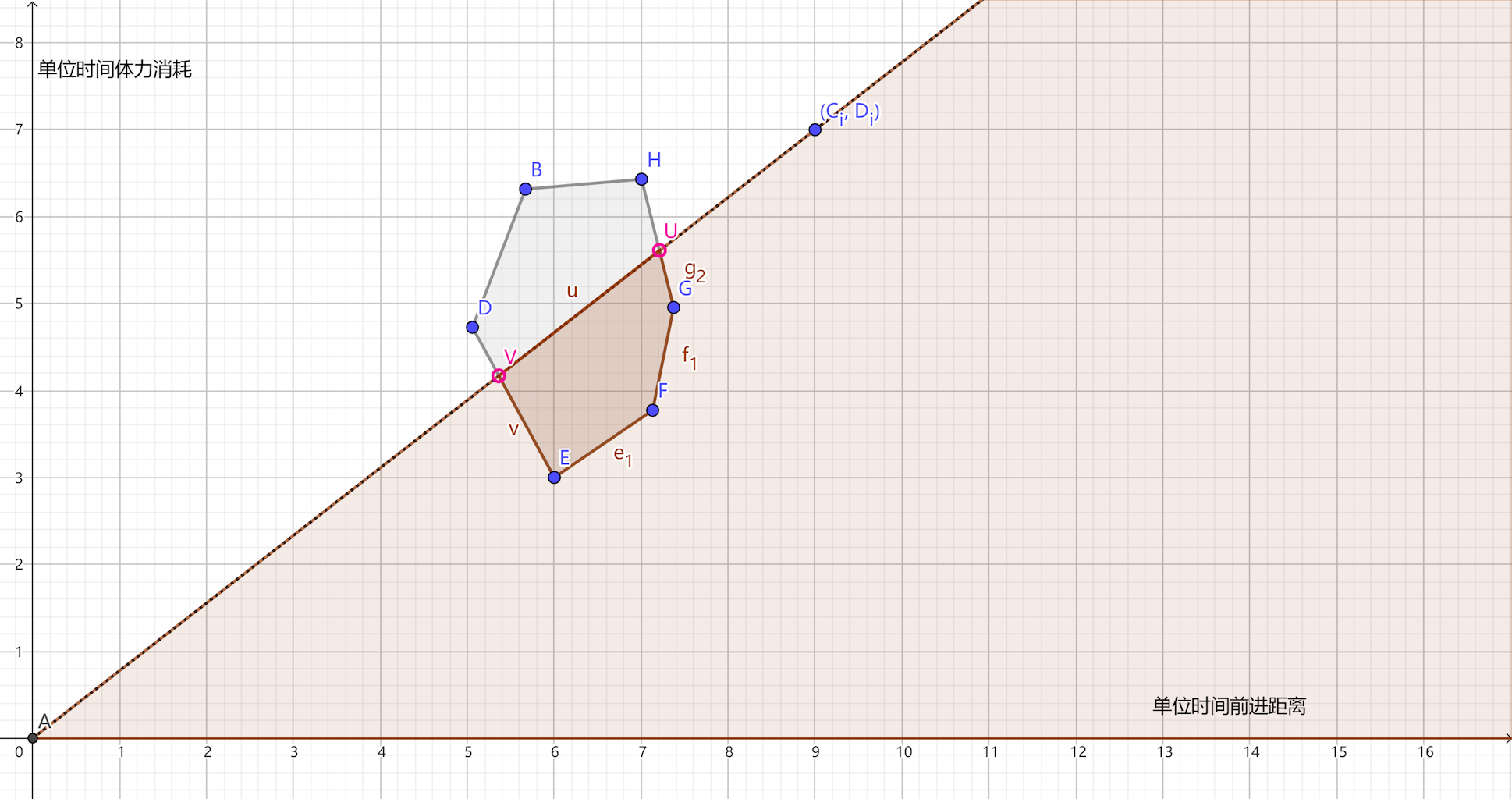
- 鉴于数据规模庞大，并且时间 \(t_i\) 是实数，传统的动态规划方法不适用。在处理每次询问时，我们需要同时考虑距离、体力和时间三个变量。一个有效的方法是转化这些变量为单位时间内的距离（即速度）和单位时间内的体力消耗。如果单位时间内的距离大于单位时间内的体力消耗，那么理论上我们可以到达终点。接下来的目标是在所有可能的情况中找到最大的速度，作为最终答案。
以两种游泳技术（N=2）为例进行具体分析。假设在总游泳时间中，技术1和技术2的使用时间比例分别为 \(p\) 和 \(1-p\) （其中 \(0 \leq p \leq 1\) ）。在这种情况下，每秒前进距离为 \(A_1 \cdot p + A_2 \cdot (1 - p)\) ，体力消耗为 \(B_1 \cdot p + B_2 \cdot (1 - p)\) 。
-
代码实现 - 并不高效
-
实现步骤
- 求出所有 \((A_i, B_i)\) 点所构成的凸包
- 对于每一个查询Q，从零点画出斜率为 \(D_i / C_i\) 的射线
- 如果凸包位于射线的“上方”，则没有满足条件的情况，返回-1
- 如果凸包位于射线的“下方”或与射线相交，则需要找到凸包在射线“下方” \(B_i\) 值最大的点。意味着这个组合可以成功到达终点，并且平均速度最快
-
复杂度分析
- 对于每一次查询，我们都要遍历凸包的所有边（即“凸包壳”）与射线的交点。时间复杂度 \(O(n)\) 。
- 对于所有查询，时间复杂度为 \(O(q * n)\) ，明显是会超时的。
-
-
优化的可能性
- 易知，并不是凸包的所有部分都能得出最优解。与原点连线斜率越小的点，其“性价比”越高，即在消耗更少的体力的同时，可以游更远的距离。
同时，如果凸包内部的某一个点满足条件，则总有位于凸包壳上面的另一个点与它更优。同样，如果凸包壳上有两个点的斜率相同，那么 \(B_i\) 值更大的点是更优的。
所以优化的目标在于找到一系列凸包壳，使其可以只保留最优解所在的边，并且排除所有非最优的情况。
我们可以从“性价比”最好的点开始，因为对于一个查询，如果所需要的“性价比”高于我们所有的选项，那么一定没有解。
然后我们逆时针遍历所有点，直到找到 \(B_i\) 值最大的点，因为对于一个查询，在满足“性价比”的情况下，这是我们能给出的，消耗时间最小的答案。 -
实现方案1:
- 我们可以使用凸包算法，找到凸包壳，按照上文所述的方法，找到斜率最小（所谓“性价比最高”）的点，然后逆时针遍历到 \(B_i\) 最大的点。这些点必然以斜率从小到大排序。 对于一个查询 \((C_i, D_i)\) ，我们将其视为斜率为 \(D_i / C_i\) 的射线。我们使用二分法，找到与该射线相交的凸包壳边。再通过联立方程方法找到其交点 \((A_x, B_x)\) ，其中 \(A_x\) 即为满足查询条件的最大游泳速度。
-
实现方案2：
- 方案2与方案1类似，只是在查找凸包的时候，加入点 \((0, 0)\) 与点 \((max(A_i), INF)\) 。如下图所示，加入这两个点之后，非最优解的点都被包含在了凸包（蓝色）内部。我们在找到凸包之后，将加入的点删除，并按方案1的方法排序。后续再进行二分，以及求交点等操作。
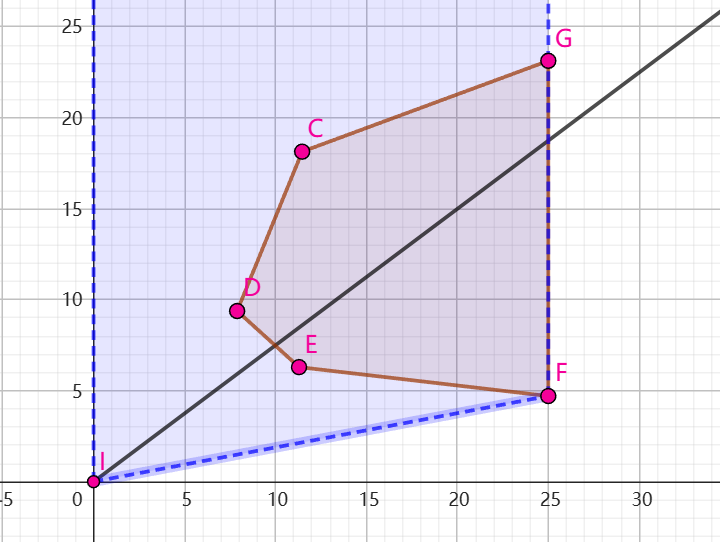
- 易知，并不是凸包的所有部分都能得出最优解。与原点连线斜率越小的点，其“性价比”越高，即在消耗更少的体力的同时，可以游更远的距离。
同时，如果凸包内部的某一个点满足条件，则总有位于凸包壳上面的另一个点与它更优。同样，如果凸包壳上有两个点的斜率相同，那么 \(B_i\) 值更大的点是更优的。
-
代码实现
-
感悟
- 别调计算几何，会变的不幸（
Comments
comments powered by Disqus