什么是容斥原理
容斥原理是一种计数手段。例如在下图中,我们想不重复、不遗漏的求出包含在ABC三个集合中所包含的元素的个数,应该使用怎么样的方法呢?
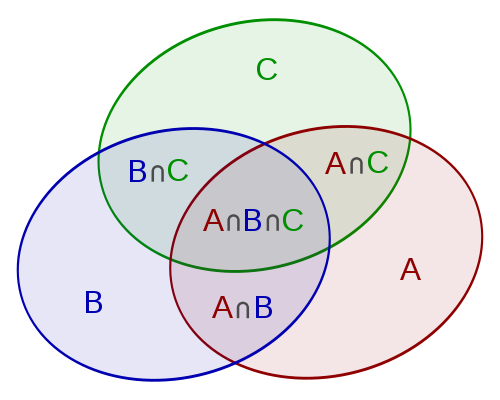
这个问题对于我们来说并不陌生,当然也并不困难。直观的方法是把所有的元素计数,再把重复的元素排除出去。这种计数的方法,有“容”有“斥”,我们讲其称做“容斥原理”。
容斥原理的应用
小规模的计数问题自然难不倒我们,我们甚至可以使用visit[]数组来记录某元素是否出现。但是当问题的规模增大时,使用数组记录这种方式需要使用更多的内存,在很多情况下,这是我们不能接受的。
考虑一个问题
问题:统计在1~N中的,能被2或3整除的数。(1 <= N <= 1e9)
我们先把这个问题拆成两部分来看:
- N以内的,能被2整除的数
- N以内的,能被3整除的数
这两个问题都非常简单,我们可以直接使用除法进行求解,其结果分别为N/2和N/3。
与此同时,我们不能忽略同时能被2和3整除的数。这里我们先求得2和3的最小公倍数6,然后应用容斥原理,将重复计数的,能同时被2和3整除的数减去,即得到最后的结果。
一个更复杂的问题 (HDU-2204,Eddy的爱好)
给你一个正整数N,确定在1到N之间有多少个可以表示成M^K(K>1)的数。 (1 <= N <=1e18)
这里我们先考虑K=2和3时的情况。对于正整数N,我们有pow(K, 1.0/2)个数可以表示为2^K;有pow(K, 1.0/3)个数可以表示为3^K。这个原理非常简单,这里不做展开。
但是,对于N=64来说,既可以表示为4^3,又可以表示为8^2。那么在上面计数的时候一定出现了重复计数的情况。所以根据容斥原理,我们将所有6的乘方全部排除。
那么对于N=4096的情况,它可以表示为2^12。那么在计数中我们是否需要考虑12的乘方呢?答案是否定的,因为12的乘方一定是6的乘方,这种情况我们已经处理过了,所以不需要再次处理。推而广之,若K可以分解质因数为a^k1 + b^k2 + c^k3,当且仅当k1 == k2 == k3 == 1时,我们才进行计数。
现在我们考虑更普遍的情况,对于任意K,我们先对其进行质因数分解。根据容斥原理,当其质因数的个数为奇数时,我们对其进行计数;为偶数时,我们从计数中排除这种重复情况。
更多的例题
计数:不能被集合里的数整除的数(HDU - 1796)
给定一个正整数集合,求在1~N中,有多少个数不能被集合中的数整除。
这道题是第一个例子的扩展。我们枚举集合的子集合,并求出子集合的最小公倍数,使用容斥原理进行计数即可。
计数:集合中至少有一对数的最大公约数为1的集合数(POJ - 1091)
求大小为N+1的集合A[N + 1],对于任意A[i]有 A[i] <= M,且A[N + 1]一定包含整数M,集合内的数可以重复。问有多少数这样的集合,使得集合中至少有一对数的最大公约数为1。
这道题的关键在于每一个集合都必须包含M。我们可以反向求解,“至少有一对的最大公约数为1”的否命题为“所有的数对的最大公约数均不为1”。这里枚举所有的最大公约数的值,并且使用容斥原理排除重复记数。
计数:平面上斜率不同的点(HDU - 2841)
给定整数N、M。求一共有多少种不同的k=n/m,使得 1 <= n <= N,1 <= m <= M。
因为k=n/m,所以在n和m的取值不互质时,我们可以将其进行约分,就会产生可能的计数重复。所以本题可以转化为求“一共有多少对互质的n、m”。我们可以枚举m来求n,就又可以转化为“对于给定的m,有多少个n与其互质”。此时可以对m进行分解质因数,使用容斥原理进行统计。
容斥原理 + DP (Leetcode - 920. Number of Music Playlists)
给定N种不同的元素,让你生成一个长度为L的列表,问有多少种不同的列表组合满足:
1. 所有的元素至少出现一次
2. 相同的元素之间至少距离K
本题的难度在于“所有的元素至少出现一次”,如果无脑DP的话,我们需要使用一维的DP来记录元素出现的情况。不过我们可以忽略这个条件,直接求意为“长度为L的列表,有多少个组合满足相同元素之间至少距离K”。这个问题我们可以使用O(N)的DP来解决。
此时的问题是我们求出来的结果可能不满足“所有的元素至少出现一次”,也就是说我们的列表里可能有不足N个元素。此时我们使用容斥原理,减去列表中不足N个元素的情况。
如果我们来出题…
对于容斥原理,如果我们站在出题人的角度,可以将其应用在如下几类“求并集的大小”的(伪)数论问题上:求能被集合中的数整数的数、求能表示为集合中的数的乘方的数、求与给定的数互质的数等。也可以用来配合DP求组合数。
但无论包装成什么样子的题目,如果它的核心是一个计数问题,并且涉及到“求并集的大小”,我们就可以尝试使用容斥原理来求解。
Comments
comments powered by Disqus